Linguagem C - Árvores Binárias
Neste artigo, falarei sobre o que é e como implementar uma estrutura de dados chamada Árvore Binária. Com tempos de pesquisa, inserção e remoção expressivamente melhores que de listas encadeadas, esta estrutura é usada principalmente em bancos de dados e sistemas de arquivos.
[ Hits: 53.446 ]
Por: Enzo de Brito Ferber em 07/05/2015 | Blog: http://www.maximasonorizacao.com.br
Introdução
O que são árvores binárias
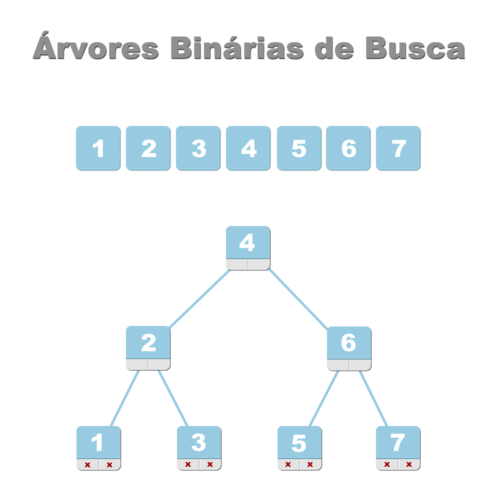
Árvores binárias são estruturas de dados usadas para organizar um conjunto de informações de forma eficiente na memória do computador. Assim como as listas encadeadas e duplamente encadeadas, árvores binárias podem conter grandes quantidades de elementos, mesmo em computadores cuja memória esteja fragmentada (sem espaço para alocar uma matriz, por exemplo).Também são bastante similares às listas duplamente encadeadas em sua estrutura básica. Todo nó de uma árvore binária contém, ao menos, um item chave (que poderá ser um int, char, char *, etc) e dois outros ponteiros: um para a subárvore esquerda e outro para a subárvore direita. Árvores binárias têm a seguinte estrutura:
struct no {
int info;
struct no *esquerda;
struct no *direita;
};
Porque usar árvores binárias?
- Custos :: Assim como as listas encadeadas, as árvores binárias precisam de relativamente pouco espaço a mais em uma estrutura, para que sua implementação seja possível. É um pequeno custo a se pagar por um benefício gigantesco. Logo, o custo/benefício é excelente.
- Implementação :: É complicado entender perfeitamente o conceito por trás das árvores binárias a primeiro momento, mas depois de um tempo, sua natureza recursiva torna as rotinas de operação extremamente simples. Como veremos mais à frente, os códigos para inserir e procurar são bem simples, deixando quase toda a complexidade para o código de remoção.
- Performance :: Listas duplamente encadeadas têm tempos de inserção, pesquisa e remoção bem ruins. No pior caso, em uma lista com 'n' elementos, você precisará analisar todos os 'n' elementos da lista. Imagine uma lista com 100 milhões de registros? (Como uma lista de emails ou a lista de cidades no mundo inteiro em uma tabela de banco de dados). Demoraria muito! Já as árvores binárias têm uma propriedade interessante: os tempos de inserção, remoção e procura, são, no pior caso "lg(n + 1)" (isto é, log de 'n' na base 2). Para os que não se lembram dos logaritmos, aqui vai uma pequena fórmula:
Isso significa que uma árvore binária (balanceada) possibilitará um tempo de pesquisa fenomenal no pior caso. Em 100 milhões de elementos, as rotinas farão no máximo 27 comparações!
- lg (100.000.001) ~= 27
- 2^27 = 134.217.728
Tipos de árvores binárias
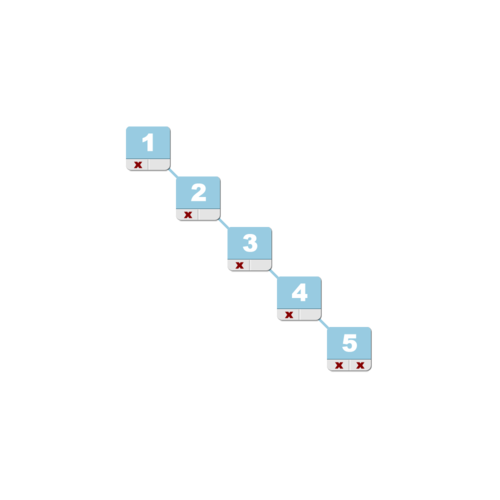
Árvores binárias possuem diversas classificações e é importante saber sobre algumas, para entender o algoritmo implementado. No nosso caso, vamos implementar uma árvore binária de busca simples. Isso quer dizer que ela não se balanceia automaticamente e que pode ser degenerada em uma lista encadeada.Os algoritmos que tornam e mantêm as árvores binárias em sua plena eficiência, são também os mais complexos. Um destes algoritmos se chama AVL (abreviação do nome de seus criadores) e o outro chama-se Rubro-Negro (Red-Black Trees). Existem outros algoritmos igualmente complexos (ou mais) e também existem outros tipos de implementações de árvores que tiram vantagem até das linhas de cache do processador, aumentando ainda mais a performance da estrutura!
O objetivo principal de todos estes algoritmos é sempre manter a árvore balanceada e maximizar a performance, para que as funções de inserção, remoção e procura, sempre sejam " O(lg(n))" e para que as árvores não se degenerem em listas encadeadas. O AVL mantém a árvore binária balanceada de acordo com a diferença entre as alturas de duas subárvores, já o RedBlack dá "cores" às raízes e realiza balanceamentos de acordo com essas cores.
Este artigo mostra como são implementadas as árvores binárias da maneira mais simples possível, o que significa que elas podem se degenerar em listas encadeadas caso os itens sejam inseridos de forma sequencial. Como dito, os algoritmos para implementar árvores binárias de busca balanceadas são mais complexos, longos e é um ótimo tema para um futuro artigo.
Nomenclatura
Árvores binárias têm sua própria nomenclatura e representação.- Uma árvore tem uma raiz e essa raiz possui nós (ou filhos, se preferir).
- Imagine a raiz como "virada para o céu" (árvore de cabeça para baixo).
- A árvore cresce para "baixo".
- Quando percorremos a árvore nos distanciando da raiz, estamos subindo a árvore.
- Quando percorremos a árvore em direção à raiz, estamos descendo a árvore.
- Nós, que não possuem nenhuma subárvore, são chamados de folhas.
Neste artigo, chamarei a estrutura base da árvore de Folha - por motivos de simplicidade (e, principalmente, porque não gosto de escrever "noh"). Mas, tudo isso é apenas questão de nomenclatura. Você não precisa saber disso para entender como as árvores funcionam, mas é sempre bom saber.
Também vale dizer que o termo certo para o ato de percorrer cada nó de uma árvore é Transversalização da árvore, mas por motivos de simplicidade, vou sempre dizer percorrer a árvore ou percorrer os nós. É necessário saber que existem três tipos diferentes de transversalização, são eles: ordenado, pré-ordenado e pós-ordenado.
Tomando como exemplo a árvore ilustrada no início dessa introdução, as transversalizações nela, seriam:
- ordenado : 1 2 3 4 5 6 7
- pré-ordenado: 4 2 1 3 6 5 7
- pós-ordenado: 1 3 2 5 7 6 4
Boa leitura!
2. Recursividade
3. Inserção
4. Pesquisa
5. Remoção
6. Transversalização
7. Conclusão
8. Código Completo e Comentado
Linguagem C - Listas Duplamente Encadeadas
Linguagem C - Funções Variádicas
Linguagem C - Listas Duplamente Encadeadas
Dicas para aprender programação
Análise dos Métodos de Ordenação usados em Algoritmos Computacionais
Parabéns pelo trabalho, dissertação completa sobre o assunto.
Primeiramente, parabéns pelo artigo.
Segundo, gostaria de saber que programa utilizou para fazer as imagens. Abraço.
[4] Comentário enviado por pablomrg em 09/05/2015 - 21:09h
Primeiramente, parabéns pelo artigo.
Segundo, gostaria de saber que programa utilizou para fazer as imagens. Abraço.
Bom dia.
Para as imagens usei o primo rico do GIMP! Filho da Adobe!
[]'s
Parabéns pelo trabalho, a parte conceitual está muito clara da para a estrutura da arvore, mas eu queria tirar um duvida se for possível, como inserir um conjunto de elementos na árvore no caso quando o campo info é um ponteiro que deverá receber elemento tipo inteiro,float e um ponteiro char para nome.
Desde já grata,
[6] Comentário enviado por dianaluz92 em 12/05/2015 - 15:08h
Parabéns pelo trabalho, a parte conceitual está muito clara da para a estrutura da arvore, mas eu queria tirar um duvida se for possível, como inserir um conjunto de elementos na árvore no caso quando o campo info é um ponteiro que deverá receber elemento tipo inteiro,float e um ponteiro char para nome.
Desde já grata,
Boa tarde.
Pelo que entendi, você quer usar árvores para armazenar uma estrutura sua, certo?
typedef struct data {
int i;
float f;
char *nome;
} data_t;
Coloque os ponteiros direita e esquerda na estrutura que está usando.
typedef struct data* data_t;
struct data {
int i;
float f;
char *nome;
data_t esquerda, direita;
};
Agora é só modificar as funções inserir(), deletar(), procurar(), imprimir(), etc.
if (!raiz) {
...
} else if (strcmp(raiz->nome, nome_ptr) > 0) raiz->direita = inserir(raiz->direita, nome_ptr);
else if (strcmp(raiz->nome, nome_ptr) < 0 ) raiz->equerda = inserir(raiz->esquerda, nome_ptr);
else {
// strcmp() == 0
// dado existente
printf("dado existente!");
return raiz;
}
return raiz;
Espero ter ajudado,
[]'s
Enzo Ferber
Bom dia Enzo,
Parabéns pelo texto. Vejo que hoje muitos do meio acadêmico não tem nem de longe a sua didática - até porque para ser didático, um professor precisa ser profundo conhecedor do tema.
Eu fiz faculdade em 2003 na PUC-Goiás e me recordo das aulas de ICC2 onde fizemos este caso de B-tree. Logo depois a grade mudou, e o curso afundou em total decadência.
Hoje vejo que muitos alunos se formam bacharéis sem ao menos entender o conceito das árvores binárias. Sem entender o que é um ponteiro, endereço de memória - afinal as faculdades estão pondo Java no lugar do C. Moral da história? Os alunos se formam e não sabem programar - então terminam seus cursos e ficam desempregados e não entendem porque nenhum empresa os querem contratar.
Obrigado por compartilhar conosco este material e seu conhecimento!
[8] Comentário enviado por Ragen em 13/05/2015 - 08:41h
Bom dia Enzo,
Parabéns pelo texto. Vejo que hoje muitos do meio acadêmico não tem nem de longe a sua didática - até porque para ser didático, um professor precisa ser profundo conhecedor do tema.
Eu fiz faculdade em 2003 na PUC-Goiás e me recordo das aulas de ICC2 onde fizemos este caso de B-tree. Logo depois a grade mudou, e o curso afundou em total decadência.
Hoje vejo que muitos alunos se formam bacharéis sem ao menos entender o conceito das árvores binárias. Sem entender o que é um ponteiro, endereço de memória - afinal as faculdades estão pondo Java no lugar do C. Moral da história? Os alunos se formam e não sabem programar - então terminam seus cursos e ficam desempregados e não entendem porque nenhum empresa os querem contratar.
Obrigado por compartilhar conosco este material e seu conhecimento!
Bom dia, Ragen.
Em primeiro lugar, muito obrigado pelos elogios.
Segundo, concordo plenamente com você (Muita gente e eu, na verdade). Uma dessas pessoas é o CEO do StackExchange, que possui um blog muito bom. O nome dele é Joel Spolsky e o blog é o http://www.joelonsoftware.com. Ele escreveu um artigo precisamente sobre a troca de linguagens "mais baixas" pelo Java nas faculdades, e como isto está arruinando o mercado de trabalho e a qualidade dos profissionais. O artigo chama-se "The Perils of JavaSchool". Excelente texto, vale a pena ser lido. (O blog todo, na verdade)
http://www.joelonsoftware.com/articles/ThePerilsofJavaSchools.html
Pessoalmente, acredito que todos deveriam ter um semestre em Assembly para entender como a CPU/Memória/HD funcionam e interagem - como tudo realmente acontece "embaixo do capô". Faz uma falta danada!
Sobre Joel: http://www.joelonsoftware.com/AboutMe.html
StackExchange: http://www.stackexchange.com
*
http://blog.codinghorror.com/why-cant-programmers-program/
Artigo muito bom também, falando sobre bacharéis que não conseguem programar programas *simples*! Leitura recomendada!
[]'s
Enzo Ferber
[9] Comentário enviado por EnzoFerber em 13/05/2015 - 09:04h
[8] Comentário enviado por Ragen em 13/05/2015 - 08:41h
Bom dia Enzo,
Parabéns pelo texto. Vejo que hoje muitos do meio acadêmico não tem nem de longe a sua didática - até porque para ser didático, um professor precisa ser profundo conhecedor do tema.
Eu fiz faculdade em 2003 na PUC-Goiás e me recordo das aulas de ICC2 onde fizemos este caso de B-tree. Logo depois a grade mudou, e o curso afundou em total decadência.
Hoje vejo que muitos alunos se formam bacharéis sem ao menos entender o conceito das árvores binárias. Sem entender o que é um ponteiro, endereço de memória - afinal as faculdades estão pondo Java no lugar do C. Moral da história? Os alunos se formam e não sabem programar - então terminam seus cursos e ficam desempregados e não entendem porque nenhum empresa os querem contratar.
Obrigado por compartilhar conosco este material e seu conhecimento!
Bom dia, Ragen.
Em primeiro lugar, muito obrigado pelos elogios.
Segundo, concordo plenamente com você (Muita gente e eu, na verdade). Uma dessas pessoas é o CEO do StackExchange, que possui um blog muito bom. O nome dele é Joel Spolsky e o blog é o http://www.joelonsoftware.com. Ele escreveu um artigo precisamente sobre a troca de linguagens "mais baixas" pelo Java nas faculdades, e como isto está arruinando o mercado de trabalho e a qualidade dos profissionais. O artigo chama-se "The Perils of JavaSchool". Excelente texto, vale a pena ser lido. (O blog todo, na verdade)
http://www.joelonsoftware.com/articles/ThePerilsofJavaSchools.html
Pessoalmente, acredito que todos deveriam ter um semestre em Assembly para entender como a CPU/Memória/HD funcionam e interagem - como tudo realmente acontece "embaixo do capô". Faz uma falta danada!
Sobre Joel: http://www.joelonsoftware.com/AboutMe.html
StackExchange: http://www.stackexchange.com
*
http://blog.codinghorror.com/why-cant-programmers-program/
Artigo muito bom também, falando sobre bacharéis que não conseguem programar programas *simples*! Leitura recomendada!
[]'s
Enzo Ferber
Opa Enzo,
Valeu pela dica. Eu já conhecia o StackExchange, mas não conhecia o blog do fundador - estou lendo os links que recomendou, realmente ótima leitura!
Se tiver Linkedin, me adiciona lá: https://www.linkedin.com/profile/view?id=80923831
Pessoal,
Na página 4 há um erro. Na função pesquisa esqueci de fazer justamente a comparação que identifica o elemento procurado.
Para utilizar a função corretamente, favor fazer a seguinte modificação:
Após a linha "if (!raiz) return NULL;"
Colocar:
else if (raiz->info == info) return raiz;
É isso.
[]'s
Patrocínio
Destaques
Artigos
Bluefin - A nova geração de ambientes de trabalho Linux
Como atualizar sua versão estável do Debian
Cirurgia para acelerar o openSUSE em HD externo via USB
Dicas
Quer auto-organizar janelas (tiling) no seu Linux? Veja como no Plasma 6 e no Gnome
Copiando caminho atual do terminal direto para o clipboard do teclado
Script de montagem de chroot automatica
Tópicos
Conselho distribuiçao brasileira (6)
archlinux resolução abaixou após atualização (15)
Não consigo instalar distro antiga no virtualbox nem direto no hd (33)
Top 10 do mês
-

Xerxes
1° lugar - 147.330 pts -

Fábio Berbert de Paula
2° lugar - 64.591 pts -

Buckminster
3° lugar - 22.270 pts -

Alberto Federman Neto.
4° lugar - 20.259 pts -

Mauricio Ferrari
5° lugar - 19.669 pts -

edps
6° lugar - 17.978 pts -

Daniel Lara Souza
7° lugar - 17.459 pts -

Andre (pinduvoz)
8° lugar - 15.995 pts -

Alessandro de Oliveira Faria (A.K.A. CABELO)
9° lugar - 15.596 pts -

Jesuilton Montalvão
10° lugar - 14.761 pts